Seeing
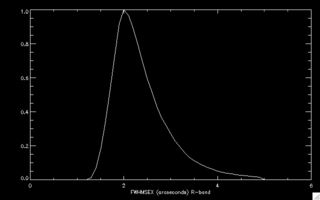
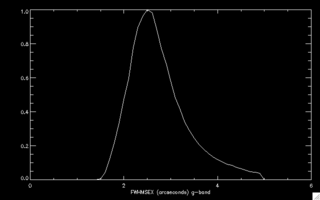
The telescope is automatically focussed at the beginning of each night. The mode of the seeing for all data in the second data release is 2 arcseconds at R-band and 2.5 arcseconds at g-band. Since each of the 12 CCDs lies in a different location in the telescope focal plane and has been leveled slightly differently, the image quality (beam size) varies significantly across the entire camera field of view. The best chips (4,5, 9) have 10% better seeing than average, while the worst (1, 7, 11) are larger by 10%. Two seeing estimators are included in the PTF headers: SEEING and FWHMSEX. Users should use FWHMSEX. It is computed from the the extracted aperture catalog, windowing the high S/N detections and computing the peak of the histogram. SEEING is computed by the camera data quality system at the telescope, and is a more simple measurement of chip 4, which is then copied to all the chips.
 |
 |
|
Normalized R-band (left) and g-band (right) histogram of the measured seeing for all CCD images in the second data release (DR2). Individual CCDs may vary by 10% from the mean for that exposure. |
|
Astrometric Calibration Methodology
Astrometric calibration is provided for all PTF data products. The final calibration is ultimately based on the SDSS-DR10, and where not available on a fallback to the UCAC-4. All PTF CCD images are independently astrometrically calibrated. Unlike space missions, various factors lead to an independent distortion fit for all images, the chief among these being the atmospheric dispersion.
Astrometry is stored in two forms in the headers. Both are polynomial expansions used to describe the distortion terms in the images. The first is the "PV" system used by the Terapix software suite (Sextractor, SWARP, etc). The second is the "TAN-SIP" model, developed for Spitzer and widely used in many astronomy packages. Both are present and usable at the same time. Note that we have seen some reports of software incompatibility because the PV system defines a keyword now reserved by the FITS standard. Deletion of the PV keywords from the header should cure this.
Astrometric Calibration Accuracy
The quality of astrometric calibration is checked by numerous means throughout the pipeline. Critically, a check is made against 2MASS at the end of the pipeline. All sources seen by PTF within a certain magnitude range will necessarily have been detected by 2MASS, and a check is made to ensure that they are, within a tight error ellipse. An additional check is made to ensure that the unit vectors for the pixel scale lie within rational bounds throughout the image. This ensures that no erroneous high distortion terms are present, which may affect only a small region of the image.
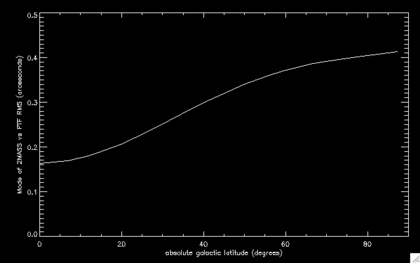
When the automated data quality system matches PTF and 2MASS sources (with appropriate magnitude windowing), it also computes the RMS scatter for those sources. This value is the mean observed offset between PTF and 2MASS and represents the "typical" error in position for a source in that image. Analysis of the PTF-DR2 data indicates that the RMS scatter in relation to 2MASS is a strong function of galactic latitude. This is probably a function of the density of stars used to generate the distortion function. The mode of the 1-sigma RMS is shown in the figure below. For any given image this is the most likely positional error, although for a given galactic latitude any given image may be somewhat better or worse. This measurement includes the underlying scatter in 2MASS as well, and so overestimates the true error in the PTF calibration. Given the typical beamsize for PTF, the positional errors are 0.1-0.4 beams.
 |
|
2MASS vs PTF positional RMS as a function of galactic latitude. |
A small number of released images (2%) have notable astrometric calibration issues: they have either failed the pixel vector test, indicating a non-physical twist or warp in the WCS solution, or they lie outside the 5-sigma distribution for 2MASS-PTF positional RMS, typically indicating an alignment failure. They are nonetheless released as they may still be useful, but will require further hand reduction. These images are identifiable by having non-zero infobit values. Infobits is discussed here.






